地理の勉強で地図は絶対に必要です。
地球はほぼ球形なのですが、球形を教科書やノートや参考書やパソコンの画面などの平面に表現することはとても難しいのです。
球形(立体)のものを平面で表現すると、どうしても様々な誤差が出てきます。
今回は地球の様子を表現する「地図」の特性についてお話ししたいと思います。
地図が表現する基本的な要素として、面積・距離・角度・方位の4つの要素があげられています。くわしいことは高校の地理の時間に勉強しますが、中学生の皆さんが勉強する地図の図法も基本的にはその特徴を理解することが大切です。どの図法にも長所と短所があります。そこをしっかりと押さえていくようにします。
さて、中学生の皆さんは、以下の3つの図法を覚えておけばよいです。
- メルカトル図法
- モルワイデ図法
- 正距方位図法(せいきょほういずほう)
以下、くわしく見ていきたいと思います。
地図の種類
メルカトル図法
メルカトル図法は、経線(けいせん)と緯線(いせん)が直角に交わっています。経線(けいせん)というのは下の地図上のたてひ引かれた南北の線のことを言い、緯線(いせん)とは地図上の横に引かれた東西の線のことを言います。
まず地図を見てみましょう。
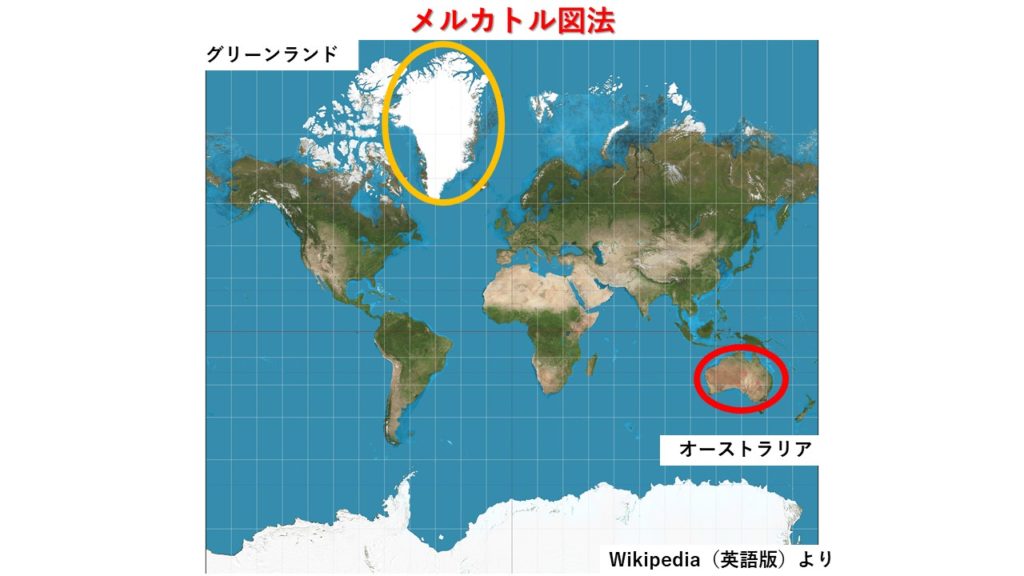
経線(南北のたての線)と緯線(東西のよこの線)とが直角に交わっていることが分かると思います。
メルカトル図法の地図は、西暦1569年にメルカトルが出版した世界地図に初めて用いられました。15世紀末に大航海時代が始まり、ヨーロッパ人が海を渡って地球上の様々な場所へ行くようになりました。世界のどこにいても正確に方角が分かるようにと航海に使える地図として考えられました。具体的にどのように使うのかというと、例えば東京からハワイまで船で移動するとします。東京からハワイまでを直線で延ばし、その線と経線(たての線)との角度を計測します。すると105度と出ます。だから、東京からハワイまで経線に対して105度の方向に向かえば、ハワイに到達できるというわけです。
欠点は、高緯度地方ほど距離や面積が拡大される傾向にある点です。
上の地図を見てください。グリーンランドとオーストラリアの場所は分かりますか?オーストラリアは世界で最小の大陸でした。グリーンランドは世界で一番広い島としても有名な島です。オーストラリアとグリーンランドの面積を比較してみます。メルカトル図法の地図だけを見ると、オーストラリアよりもグリーンランドの方が広い感じがしますよね。ところが、実際に面積を計測してみると、
- オーストラリアの面積:約759万4700平方km
- グリーンランドの面積:約216万6000平方km
という感じです。地図の見た目と比べるとどうですか?全然違いますよね?面積に誤差がありますよね?
また、赤道の長さと高緯度地方の緯線(地図上の東西の線)の長さも違います。赤道の長さは1周が約4万キロなのに対して緯度60度だとその半分になります。しかし、メルカトル図法の地図で見ると、赤道の長さも緯度60度の長さも全部同じですよね。この点においても誤差があることが分かりますよね。
最後に地図の4要素にメルカトル図法の特徴を当てはめてみましょう!
- 面積:不正確
- 距離:不正確
- 角度:正確
- 方位:不正確
正距方位図法
正距方位図法(せいきょほういずほう)とは、地図の中心からの距離と方位が正しく示される図法の地図のことです。漢字をそのまま暗記しない。名前には意味がちゃんとあるので、漢字と意味をかみしめながら、図法の名前を覚えていきましょう。
正距方位図法の地図を見てみましょう。

実は国際連合(United Nations)の旗にも正距方位図法が使われているんですね。
正距方位図法の急所は、中心からの距離と方位が正確だという点です。だからメルカトル図法が海図に使われていたのに対して、正距方位図法は飛行機が最短距離(大圏航路)で目的地まで到達する航路図に使われることが多いです。
一方、どこか任意の地点の2カ所の距離を正距方位図法で調べることはできません。
最後に地図の4要素に正距方位図法の特徴を当てはめてみましょう!
- 面積:不正確
- 距離:正確
- 角度:不正確
- 方位:正確
モルワイデ図法
上の「メルカトル図法」と「正距方位図法」では面積を正しく表現することはできませんでした。
そこで、面積がほぼ正しく表現できる地図の図法が考案されました。最初に出てきたのはサンソン図法というものでしたがこれを下に改良されたのが「モルワイデ図法」です。「モルワイデ図法」は西暦1805年にモルワイデによって考案されました。
[覚えなくてもよい]
緯線の40.44度の長さが正確で、それより低緯度では実際より短く、高緯度では長いです。緯線の間隔は、高緯度になるにしたがってせまくなっていきます。
実際の地図を見てみましょう。
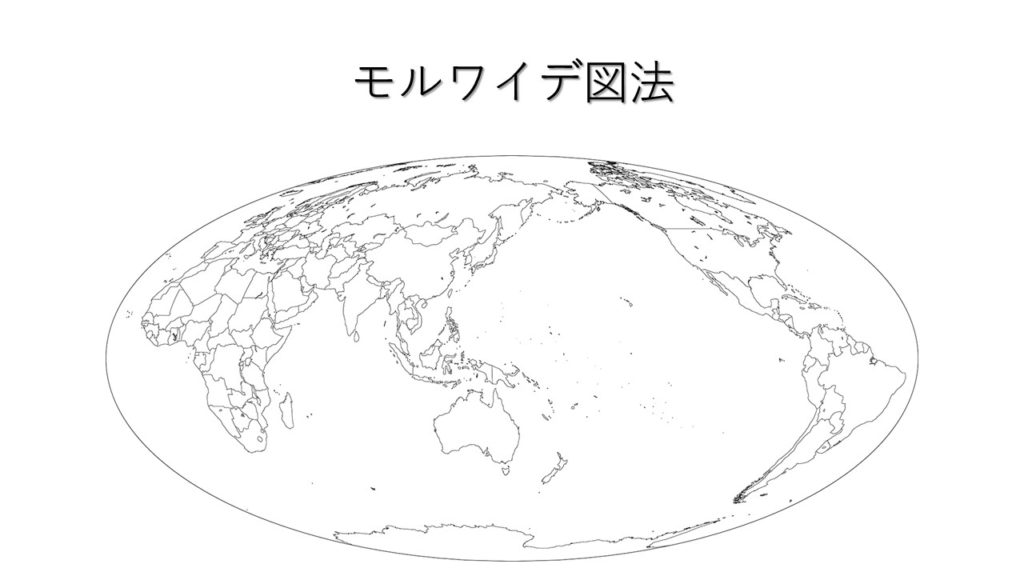
「モルワイデ図法」はこういった特徴から、主に国の大きさを把握したり、分布図として利用されることが多いです。この点も押さえておきましょう。
最後に、地図の4要素にモルワイデ図法の特徴を当てはめてみましょう!
- 面積:正確
- 距離:不正確
- 角度:不正確
- 方位:不正確
地図の4要素を正確に表現するために…(発展)
地図で表現される4要素を同時に表現できる図法は存在しません。できるだけゆがみや誤差の少ない図法を考案しようと努力がなされています。
例えば、一部の教科書に載っている「グート図法」。これは先ほど少しだけお話ししたサンソン図法とモルワイデ図法を組み合わせたものです。サンソン図法は低緯度地方のゆがみが小さい図法、モルワイデ図法は中緯度地方のゆがみが小さい図法として知られ、これらをミックスしたものです。
また、「オーサグラフ」と呼ばれる地図も考案されました。西暦1999年に日本の建築家である鳴川肇らによって考案されたものです。面積がほぼ正しく、また方位や形、距離のゆがみがこれまでよりも少ない図法です。
発展部分についてはこの記事ではくわしく触れないので、グーグルなどの検索エンジンで調べてみてください。
地球儀
面積・距離・角度・方位が正確に表現できるものといえば、やはり地球儀ですね。
家にあるという皆さんも多いでしょう。見たことがないという人はぜひ学校で見てくださいね。
復習をしっかりやろう!
復習の必要性
世の中には「授業がうまい先生」という人たちがたくさんいます。「授業のうまい先生」は皆さんを分からせる名人です。しかし、授業を受けっぱなしにしているとすぐに習ったことは忘れてしまいます。逆に教えている内容を全て忘れさせない授業が行える先生なんて存在しません。
では、習ったことを忘れないようにするためにはどうしたらよいか?というと、復習をやるしかありません!
問題集を解く!
「まほろば社会科研究室」の説明はもう一度読んで復習をすればよいのですが、問題集を使った演習を行う必要があります。
定期テスト対策やはじめから地理の勉強をやり直したいという人はこのあたりから問題を解き始めてもよいと思います。
入試対策を本格的に行いたいという人は、以下の問題集がオススメです。
問題は解きっぱなし、答え合わせをしっぱなしにするのではなく、お手元の教科書や参考書に戻って印をつけておきます。そして必ず関連知識も含めて知識の暗記をし直すようにしましょう。一問一答のような勉強をしてその問題ができるようになったとしても、違う角度から問題が出題されたら「お手上げ」状態になってしまう例をたくさん見てきました。関連知識のインプットも必ずし直すようにしましょう!